Anti-aliasing, díl II: Bojujeme proti aliasu

Analýza situace: vyšší rozlišení vs. anti-aliasing

U každého konkrétního obrazového defektu jsem vzpomněl nějaké to řešení, které by známky aliasingu mohlo zmírnit. Záměrně jsem však nezmínil jedno řešení. Jaké? Pokud shrneme rozebírané situace (aliasing), dojdeme k závěru, že všechny popsané problémy jsou způsobeny příliš velkou vzájemnou vzdáleností vzorků; mezi hodnotami barev sousedících vzorků je velký skok. A to lze řešit jednoduše. Použijeme větší množství vzorků, což znamená vyšší pokrytí (vzorky blíže sobě).

Ještě než tak učiníme, je důležité se zaměřit na ty nejviditelnější projevy aliasu. Těmi jsou jagged edges (zubaté hrany). Z následujícího obrázku je dobře vidět, že jaggies jsou nejpatrnější při nízkých úhlech (blízkých vertikále či horizontále) - červeně. Jejich viditelnost klesá (modře) až do násobků úhlu 45°, kdy je minimální (zeleně). Nyní vidíme, že nejdůležitější je se zaměřit právě na zmíněné nízké úhly.

Nyní můžeme přistoupit k samotnému kroku redukce "zubatosti". Kupříkladu zvětšíme množství vzorků 4x. To s sebou nese dilema: Použít pro každý vzorek jeden samostatný pixel (což znamená 2x vyšší rozlišení, čili 4x vyšší plochu), nebo původní rozlišení zachovat a pro každý pixel vypočítat čtyři vzorky (= vytvořit pixel zprůměrováním barvy jedné čtveřice vzorků)?

Porovnejme oba způsoby řešení problému (schéma níže):

bod A: použijme standardní rozlišení a zjistíme, že množství aliasu v obraze není akceptovatelné. Máme k dispozici dva způsoby řešení (první značený zeleně, druhý modře)

bod B: ať si vybereme první způsob nebo druhý, tento krok je prakticky společný: scénu vykreslit ve dvojnásobném rozlišení (tedy 4-násobná plocha - pro názornost jsem vpravo naznačil, že místo jednoho pixelu budou vykresleny 4).

bod C: pokud jsem šli cestou vyššího rozlišení, jsme na konci - pro zobrazení použijeme tento 2x větší obraz. Pokud jsme šli druhou cestou, schází nám poslední krok: zmenšíme tuto plochu na původní požadované rozlišení (prakticky zprůměrujeme barvu vždy čtyřech pixelů a tu použijeme pro jeden výsledný pixel)

 

 

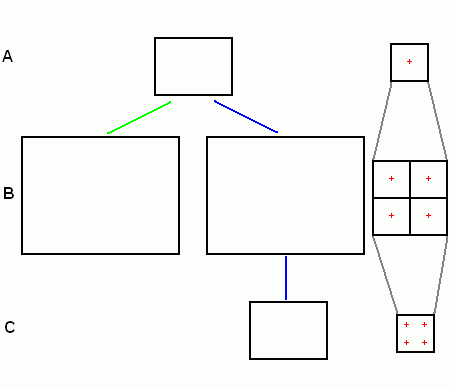
Výsledkem obou postupů je kvalitnější obraz. Na druhé straně potřebujeme spočítat čtyřnásobné množství pixelů, než jsem původně potřebovali, takže požadavky na fillrate (a vlastně celou pixelovou část) grafického systému vzrostou 4x (v obou případech). Jaká je tedy vhodnější cesta? Pokud náš zobrazovací adaptér (monitor) snese rozlišení, které je použito v bodě B, pak je prakticky zbytečné obraz zmenšovat a je lepší dvojnásobné rozlišení ponechat.

Pokud ale náš monitor vyšší rozlišení nezvládá, obraz zmenšíme na původní rozměry a zobrazíme. Tomuto způsobu se říká AntiAliasing (=AA), přesněji řečeno jde o jeden z nejstarších způsobů antialiasingu (konkrétně ordered grid super-sampling 4x provedený pomocí metody zvané oversampling - to ale rozebereme později).

Ať ale dvojnásobné rozlišení, nebo antialiasing 4x (= dvojnásobné rozlišení + zmenšení), obě metody mají svá pro i proti (čtyřnásobné požadavky na fillrate) a nelze jednoznačně říct, která je lepší. Rozeberme trochu zmíněný antialiasing 4x. Prozatím můžeme na chvilku zapomenout, že potřebujeme vykreslit dvojnásobné množství pixelů (~ vzorků), podívejme se na to z teoretické stránky:

...jak by vypadala ideální situace:

Pokud bychom nepoužívali AA, bude pro každý pixel spočten jeden barevný vzorek:

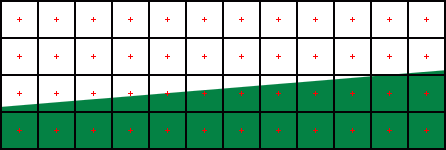
A výsledek bude vypadat takto:

 

Tentokrát ale použijeme výše popsaný AA 4x, tzn. že pro každý pixel odebereme barevný vzorek ve čtyřech vyznačených místech, tyto čtyři barvy zprůměrujeme a použijeme jako výslednou barvu pixelu:

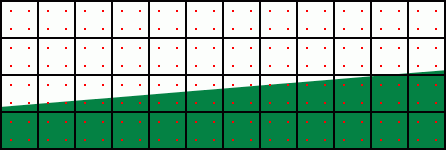
A jak bude vypadat výsledek:

 

Je vidět, že s použitím AA jsme dosáhli poněkud lepšího výsledku, než bez něj. Tam, kde by byl ostrý "schod", vznikl barevný přechod. Sice jen jednobarevný, ale rozhodně jsme dosáhli určitého zlepšení. Pokud se podíváme na rozložení vzorků, zjistíme, že jich je zbytečně mnoho a že pokud bychom použili pouze dva na pixel, byl by výsledek stejný a zároveň bychom šetřili fillrate (čtyři vzorky znamenají čtyřnásobný, dva vzorky logicky jen dvojnásobný fillrate):

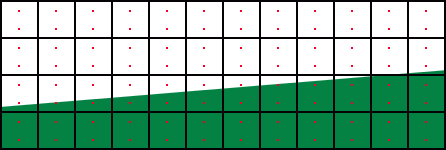
A získáme prakticky tentýž výsledek:

 

Skoro by se zdálo, že máme vyhráno, ale co když bude úhel naší zelené hrany poněkud jiný:

         

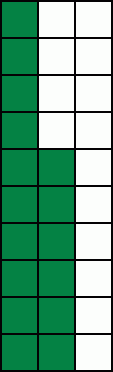
Bohužel, zde se situace obrací. Přestože jsme použili dva vzorky na pixel, dosáhli jsme stejné kvality, jako kdybychom AntiAliasing nepoužili - žádné vyhlazení se nekoná. A navíc jsme potřebovali dvojnásobný fillrate :-(. To příliš úsporné není.

Proč ale při stejném rozložení vzorků došlo ke dvěma tak diametrálně odlišným výsledkům? Vysvětlení není obtížné: všimněte si, že ve druhém případě jsou vzorky seskupeny téměř rovnoběžně s hranou, kterou chceme vyhladit. Tím se vzorky oproti hraně dostávají do jakéhosi zákrytu a nemohou být dobře využity. To ale lze snadno řešit: Rozložíme vzorky trochu jinak; tak aby se ani v jednom z "kritických" případů do zákrytu dostat nemohly. Nejlépe takto:

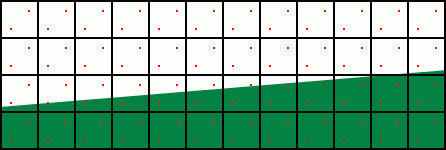
A výsledek:

Zkusme ještě, jak dopadne druhá situace:

          

Jak je vidět, dosahuje tento způsob dobrých výsledků v obou případech. Výsledek je prakticky stejný jako v případě AA 4x, ze kterého jsme na začátku vycházeli - tomu už lze říkat efektivní optimalizace: pro dosažení obdobné kvality stačí polovina vzorků, tedy poloviční fillrate.

Analogicky odvodíme rozložení vzorků, které bude ideální pro režim 4x... Máme několik možností, jak postupovat:

1) Při odvození ideálního rozložení vzorků FSAA 2x jsme vyšli z režimu s počtem vzorků 4x, tedy druhé mocnině požadovaného režimu (pro zjednodušení 2²=4) a vynechali jsme "zbytečné vzorky jen žeroucí fillrate" a to tak, aby v každém "řádku" i "sloupci" zůstal jen jediný vzorek...

Pro odvození režimu 4x tedy použijeme režim s počtem vzorků 4² - tedy 16. To vypadá nějak takto:

A vynecháme zbytečné vzorky tak, aby v každé "řádce" i "sloupci" zbyl jen jeden vzorek (celkem musí ale zbýt vzorky 4). Dostaneme se k následnému výsledku:

(Ještě bychom mohli dojít k výsledku, který vypadá oproti zobrazenému zrcadlově.) 

2) Druhý způsob odvození ideální situace: Vezmeme režim 4x a představíme si, že vzorky oproti pixelu pootočíme. A to přesně tolik, aby vzdálenost "a" mezi všemi vzorky byla stejná:

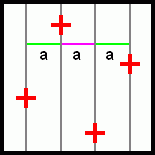
Dostáváme tentýž výsledek, jako v předchozím případě.

Snadno dojdeme k závěru, že máme režim, který nabízí kvalitu FSAA 16x, ale nároky na fillrate jsou jako při režimu 4x.

Jistě si vzpomenete na schéma, kde jsem rozebíral, zda je výhodnější použít AA 4x, nebo přímo dvojnásobné rozlišení. Výsledek byl nerozhodný. Pokud bychom ale původní AA 4x zaměnili za tento optimalizovaný režim, který při stejných nárocích na fillrate poskytne kvalitu blízkou režimu 16x (tedy až čtyřnásobnou), pak je myslím výsledek jasný - vítězí antialiasing, protože je schopen nabídnout při stejných nárocích na výkon hardwaru mnohem vyšší kvalitu.

Pozice vzorků v pixelu

V minulé kapitole jste si mohli všimnout, jak důležitou roli hraje rozložení vzorků (=subpixelů). Aby bylo možné se v těchto typech alespoň trochu orientovat, existují pro tyto pozice určité názvy (které se ale poměrně často mění - výrobci hardwaru se nás snaží "oblbnout" svým marketingem a tak nazývají staré technologie stále jinými novými jmény :-)

Všechny typy rozložení vzorků bychom mohli rozdělit do dvou skupin:

-symetrické (symetric)
-nesymetrické (asymetric)

Přestože se toto rozdělení poslední dobou celkem opomíjí, je celkem praktické a můžeme z něj vyjít dál:

Symetrické vzorkování:

-můžeme najít prvky symetričnosti - třeba osu či střed souměrnosti (v uskupení vzorků); spadá sem:

-Ordered Grid
-Rotated Grid
-Semi-Rotated Grid

Ordered Grid:

Neboli uspořádané rozložení vzorků je to, které jsem představil jako první. Vzorky jsou uspořádány pravidelně, jako by každý byl středem jakéhosi virtuálního čtverce (či obdélníku), které se vzájemně dotýkají. Lepší bude několik ukázek:

                

Toto je samozřejmě jen několik možných typů. Konkrétně 2x, 3x, 4x, 6x a 16x. Všimněte si, že v typech 2x, 3x a 6x máme vždy ještě další dvě možnosti. Ukázka:

     

Pozice mohou být ve jmenovaných případech (na obr. 2x) uspořádány vertikálně, nebo horizontálně. Podle toho určujeme, zda jde od AA 2x horizontální, nebo AA 2x vertikální. Zde je důležité upozornit na jednu nepříjemnost tohoto značení: Horizontální AA je ten, při kterém jsou vzorky rozloženy vertikálně :-). Proč? Protože pokud jsou vzorky rozloženy vertikálně, dojde k vyhlazení horizontálních linií, to znamená horizontální AA (a opačně).

Rotated Grid:

Rotated grid, čili pootočené rozložení vzorků, jsem už taktéž zmiňoval v předchozí kapitole, kde jsem ho nazýval jako "ideální" nebo "optimalizované". Způsob, jak odvodíme pozice vzorků, jsem tam rozebral taktéž. Rotated grid je rozložení splňující tyto podmínky:

Protneme-li každý ze vzorků horizontálou a vertikálou, bude na každé horizontále i vertikále ležet jen jediný vzorek; vzdálenost mezi nejbližšími horizontálami (příp. vertikálami) je konstantní. To možná zní dost složitě, obrázek pomůže:

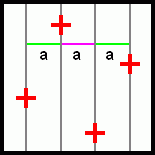
Každým vzorkem prochází jedna vertikála. Vertikály jsou od sebe stejně vzdáleny (a). Ještě bych mohl připomenout, že vzdálenost od krajních vertikál k okraji pixelu by měla být "a/2" (to aby byla vzdálenost "a" dodržena i mezi vzorky vzájemně sousedících pixelů).

Toto je ideální případ pro Rotated Grid 4x. Opět pár ukázek:

     

RG 2x, RG 4x. Samozřejmě je možné odvodit rozložení i pro vyšší počty vzorků, ale to už se objevují první problémy. Ty vycházejí i z většího počtu vzorků. Např. 6x - pokud vyjdeme z rozložení Ordered Grid 6x, které pootočíme, docházíme k výsledku, který není zcela ideální, protože vykrytí plochy pixelu není příliš rovnoměrné (zůstávají oblasti, ve kterých není vzorek).

Mohli bychom ale rozložit vzorky tak, aby byly uspořádané jako vrcholy šestiúhelníku (a následně vhodně natočit). To už by bylo výhodnější... Tím chci naznačit, že čím více vzorků máme k dispozici, tím více možností pro rozložení typu Rotated Grid existuje.

Problémem je přijít na všechny možnosti a vybrat tu nejvýhodnější... Pokud je tedy trendem budoucnosti větší množství vzorků (FSAA 8x, 16x, 24x, 32x...), pak je před námi nespočetné množství různých cest. Tato kapitola je velice dobře popsána na serveru 3dcenter.de, kde je zobrazeno poměrně dost těchto ukázek, takže pokud vám nevadí němčina, vydejte se tam (článek "Anti-Aliasing Masken" a několik dalších). Pokud se vám do němčiny nechce, dovolím si vypůjčit jen několik ukázek, jak může vypadat maska pro rotated grid 8x.

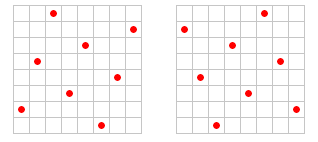
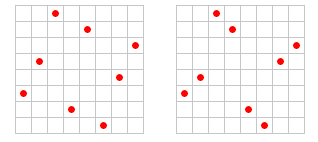
Původ: 3DCenter

Jak vidíte, už při režimu 8x je možností opravdu hodně. Při nízkých úhlech budou všechny podávat obdobné výsledky, ale rozdíly se objeví při vyšších úhlech a v účinnosti proti ostatním typům aliasu.

Semi-Rotated Grid

Částečně pootočená mřížka, skewed grid (najde mnoho různých názvů)... Prakticky ty pravidelné typy, které neodpovídají ani OG, ani RG. Už jsme si ukázali, jak je ordered grid nevýhodné a jak výhodné je oproti němu rotated grid. Tato skupina se svojí účinností "nacpe" někam mezi ty dvě předchozí. Jak tento typ snadno a rychle poznat? Pokud protneme horizontály a vertikály, bude na některých ležet jeden vzorek, na jiných třeba dva vzorky, nebo více. Opět ukázka:

     

Máme zde několik možností (1. případ už nijak jinak zobrazit nemůžeme, ale druhý ano - zrcadlové zobrazení, rotace o 90°, rotace o 90°+ zrcadlové zobrazení). Při vyšším množství vzorků drasticky narůstá množství dalších možných kombinací, takže asi nemá smysl toto téma dál rozebírat - i s přihlédnutím k tomu, že semi-rotated Grid režimy nejsou v praxi příliš rozšířeny.

Asymetrické vzorkování

Tento způsob se nepoužívá příliš dlouho (alespoň co se herních 3D akcelerátorů týče). I když... Vezměme to postupně:

-Semi Prearranged
-Prearranged
-Stochastic

Semi Prearranged Sample Location

To je název :-). Prakticky se nepoužívá, spíše narazíme na termín "SmoothVision 1.0". Což nám napovídá, že jde o něco z dílen ATI. Výrobce ale zatím nechme stranou a podívejme se, co to vlastně znamená. Částečně předpřipravené pozice vzorků... nebo jak bychom to mohli česky nazvat - je způsob, který byl pokusem o kvalitativní překonání režimu ordered grid.

To na jednu stranu není nic těžkého, ale na druhou stranu byl tento způsob poměrně krkolomným. Ukažme si, jak vypadal takový režim SmoothVision 1.0 při úrovni 4x (čtyři vzorky). Výchozím bodem je ordered grid 4x a předgenerovaná tabulka vzorků (součást ovladačů). Tato tabulka obsahuje pozice pro čtyři vzorky. V praxi je pak použit režim ordered grid a jeden ze čtyř vzorků je zaměněn za vzorek z tabulky:

Takto může vypadat připravená tabulka vzorků:

Vycházíme ze standardního rozložení ordered grid...
(vzorky jsem pro lepší názornost označil barevně)

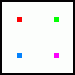
Pracujeme vždy po čtveřicích pixelů:

Vzorky pro první pixel jsou vytvořeny tak, že první ze vzorků OG nahradíme příslušným vzorkem z tabulky - tím červeným (proto to barevné značení :-) a výsledek:

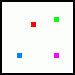
Druhý pixel ze čtveřice vznikne analogicky záměnou druhého vzorku (fialový):

Třetí... (ten modrý)

A poslední čtvrtý (zelený):

Celá čtveřice pak vypadá následovně:

No, vypadá to divně, ale pokud spočítáme horizontály a vertikály, zjistíme, že jich o 50% přibylo. A to je podstatné. Navíc tím, že není rozložení vzorků pravidelné dochází k jednomu jevu, který rozeberu později - jehož výsledkem je, že se v praxi zdá, jako by byla použita vyšší úroveň antialiasingu... Tento režim je svými výsledky zhruba srovnatelný se semi rotated grid.

Jen pro úplnost uvedu, že všechny čtveřice pixelů ve scéně pak nesou stejné rozložení vzorků jako výše zobrazená.

Prearranged Sample Location

Spíše známý pod názvem sparse sample location. Má velmi blízko k rotated grid, ale pravidelnost rozložení vzorků je mizivá. Pozice všech vzorků pixelu je připravena předem. A to tak, aby účinnost byla co nejvyšší, ale rozložení vzorků nebylo pravidelné. Platí pravidlo (zmíněné u rotated grid): protneme-li každý ze vzorků horizontálou a vertikálou, bude na každé horizontále i vertikále ležet jen jediný vzorek; s tou vzájemnou vzdáleností horizontál (či vertikál) už to není tak žhavé, vzdálenosti bývají zhruba stejné, ale nemusejí být... Pár ukázek...

          

Účinnost při nízkých úhlech je zhruba stejná, jako v případě rotated grid (tedy maximální možná). Je také možné si povšimnout, že pozice vzorků jsou akumulovány jakoby kolem úhlopříček (násobky 45°). Vzpomeňme, že účinnost AA je nejnižší právě v těch úhlech, podél nichž jsou vzorky rozmístěny. Sparse sample systém má tedy nízkou účinnost v úhlech blízkých 45°, což ale prakticky nevadí, neboť tyto úhly vyhlazování nepotřebují :-)

Přestože se tento režim může zdát výrazně výhodnější, než RG, není tomu v některých případech tak. Mohou se sem-tam objevit i situace (některé specifické úhly - nelze je souhrnně jmenovat, záleží na konkr. lokaci vzorků), kdy sparse podá horší výsledek než RG. Ty jsou ale poměrně vzácné.

Stochastic Sampling

Náhodné rozložení vzorků, náhodné vzorkování. Na poli herních akcelerátorů jde o hudbu budoucnosti. Možná bude nakonec tento režim zavrhnut, možná ne; má své zastánce i odpůrce, není jednoduché ho realizovat, ale v praxi se s ním můžeme setkat snad jen na (dnes již starších) profi akcelerátorech společnosti 3DLabs. Za určitých okolností mohl již být standardem i na běžných grafických kartách. Zatím ale nechci odbočovat.

O co se jedná: Bylo více-méně dokázáno, že použití jakéhokoli pravidelného (časově i plošně) vzorkování vede k přenosu aliasu na vyšší frekvence. Lidské oko je extrémně citlivé na pravidelnost a pozůstatky aliasu dokáže v obraze vypozorovat. Pokud by vzorkování bylo dostatečně nepravidelné, je po problému.

náhodné vzorkování (stochastic sampling) 32x
jedna z milionů možností...

Zároveň však nastává problém číslo 2. Pokud vzorky rozmístíme náhodně, může dojít k situaci, která bude krajně neefektivní (např. nahloučení všech vzorků těsně u sebe) a spíše si přihoršíme. To ale lze vyřešit. A hned několika způsoby: Můžeme třeba zajistit, aby v případě, kdy bude pozice vzorku vygenerována velmi blízko jiného vzorku, byla vymazána (nepoužita) a generována znovu.

Na druhou stranu je nutné připomenout, že tento způsob je výpočetně náročný a nelze předem určit, jak dlouho bude trvat vygenerování všech pozic pro jeden pixel. Jiný způsob... Předem bychom připravili rozsáhlou databázi náhodných rozmístění, která by byla při vykreslování využívána. Předchozí problém bychom tak měli z krku.

To ale stále ještě není vše. Pokud totiž tento systém použijeme v praxi s běžně používaným množstvím vzorků (2 či 4), pak stále bude situace horší, než při pevně daných pozicích (RG, sparse). Problém je v tom, že s malým počtem vzorků nedosáhneme přílišného vykrytí plochy pixelu, takže vzniklý šum bude výraznější a rušivější, než samotný aliasing, a proto je použití stochastic samplingu prakticky realizovatelné až od vyššího počtu vzorků - absolutní minimum je tak 8-10, prakticky použitelná hodnota je 16 a samozřejmě čím více tím lépe.

Pokud použijeme 16 vzorků, dosáhli jsme požadovaného efektu, protože alias je převeden na jemný šum a ten už oko není schopno dobře zachytit. Takže úspěch? No, zas tak velký ne. Pokud bychom oněch 16 a více vzorků použili s nějakým z ostatních systémů (RG, Sparse), dosáhli bychom zřejmě vynikajícího výsledku taktéž... Posouzení nechme na někom jiném a podívejme se na jednu ukázku od společnosti 3DLabs:

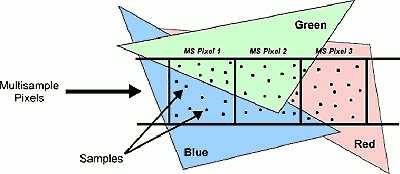
3DLabs nazýval tento systém "SuperScene" a toto je jedna z jeho prezentací. 3 pixely na třech různobarevných polygonech, kde se 3DLabs snaží dokázat přednosti tohoto algoritmu. Ale nic se nemá přehánět. Všimněte si, jak dobře vzorky dobře pokrývají ty malé úseky polygonů (červený trojúhelníček na druhém pixelu a modrý na třetím pixelu). Pokud bychom vzájemně prohodili pozice vzorků druhého a třetího pixelu, dojde naopak k situaci, kdy tyto části nebudou vůbec vykryty. Kde nestačí technologie, pomůže marketing :-)

V souvislosti s herními akcelerátory byla technologie náhodného vzorkování zmíněna dvakrát. Poprvé z úst bývalých inženýrů 3Dfx, kteří ji měli v plánu implementovat do třetí generace karet po Voodoo 5 (podrobněji zmíním v dalších kapitolách), a pak stejně neoficiálně od inženýrů ATI, kteří provedli rozsáhlé experimenty s touto metodou a došli k závěru, že systém náhodného vzorkování, který by svojí náročností nepřesahoval požadavky na množství tranzistorů vymezitelné v grafickém čipu pro herní real-time rendering, by musel pracovat s minimálně 32 (spíš 64) vzorky, aby kvalitativně překonal pevně dané vzorkování s využitím moderních psychovizuálních modelů. A byl logicky poslán k ledu.

poisson / poisson disc / jitter

Za zmínku stojí základní rozdělení:

• poisson (vzorky jsou rozloženy náhodně)

• poisson disc  (jako předchozí, následně je provedena kontrola rozložení a v případě přílišné blízkosti některých je jejich pozice upravena)

• jitter (pixel je rozdělen do několika dílů, jejichž počet odpovídá počtu vzorků; v rámci plochy každého dílu je náhodně vygenerována pozice pro jeden pixel)

Určitý hybrid metody poisson disc a jitter jsem zmiňoval začátkem roku 2004:

"Pozice vzorků by byla generována náhodně, ale pravděpodobnost umístění vzorku by byla nejvyšší v okolí pozice vzorku při RGAA (na obrázku režim 4x). Čím sytější barva, tím vyšší pravděpodobnost výskytu pozice vzorku."

Vzhledem k tomu, že není příliš pravděpodobné, že bychom se s plnohodnotnou formou náhodného vzorkování mohli v nejbližších letech setkat, nemá cenu, abychom ho dále rozebírali. Hardwarová náročnost je prozatím příliš vysoká.

V rámci této kapitoly bych ale zmínil ještě jednu zajímavou techniku. Původně se jí říkalo adaptivní antialiasing (neplést s tím, co teď nabízí ATI, jde o něco jiného!). Tento systém by byl schopen rozmístit vzorky pro každý pixel tím nejvhodnějším způsobem (tak, aby byly rozloženy podle situace konkrétního pixelu).

Může existovat bezpočet metod, jak toho dosahovat, ale většina je velmi pomalá. Např. pokrýt pixel uspořádanou skupinou 16 vzorků a podle toho, mezi kterými je odlišná barva, zhruba určit, kde se vyskytuje barevné rozhraní a podle jeho pozice znovu provést rozložení vzorků, ale pro daný pixel efektivnější.

Jiný systém zakládá na rozložení menšího množství (2-4) vzorků na každý pixel. V případě, že na každý připadne různá barevná hodnota, bude pixel renderován znovu s použitím vyššího množství vzorků. V případě, že všechny budou stejně či obdobně barevné (= pixel se nenachází na kontrastní hraně), bude tato barva rovnou použita.

Tímto dnešní kapitolu uzavírám. Existují sice i mnohé další systémy, ale ty se obvykle příliš neliší od výše jmenovaných, nebo mají k rozumné implementaci ještě daleko a není pravděpodobné, že bychom se s nimi mohli v blízké době setkat.

V minulém díle jste si měli možnost přečíst, co to vlastně aliasing je, jak vzniká a jak se nejčastěji projevuje. Dnes jsme se zaměřili na antialiasing; konkrétně na metody, jejichž cestou se ubírá vývoj a především na efektivitu různých systémů distribuce vzorků v pixelu. V příštím dílu se oproti dnešnímu trochu více odpoutáme od teorie, zmíním slepé uličky, zaměřím se na samotné metody FSAA (supersampling, multisampling a další) a dostaneme se blíže specifikům jednotlivých výrobců.